Not always sci-fi movies heed science, but sometimes scientists heed sci-fi movies too. Well, this commotion is all about cloaking devices used in fictional movies like Harry Potter and Star Trek, which are now an absolute reality. Some of the basic principles of optics are summed up to make things invisible and cloaking possible.
To start from scratch, cloaking devices are something which makes things partially or fully undetected to the electromagnetic spectrum, which entails the visible spectrum. Basic principles of cloaking involve analysis of the well-known Ray transfer matrix/ABCD matrix. By the name itself, it means that these contain matrices (mostly 2×2) which transform the initial/incident rays to the final or emerging rays from an optical device/system as depicted in the picture.
These ABCD matrices are different for different optical lens in different configurations. For a perfect cloaking device, ABCD matrix must be an identity matrix with B differing from 0 to 'L/n' where L is the length of the optical device or system, and n is the refractive index of the surrounding medium. These ABCD matrices should have determinant 1, and other diagonal element(C) must be 0, which means that if we transform object rays which are from infinity, the image rays should also converge at infinity which is termed as afocal.
So to make a cloaking device let us start from one convex lens and refractive index 1 for which the ABCD matrix will be
which is not the one required or satisfied by the matrix for the perfect cloaking device.
Moving onto two lenses the ABCD matrix will be
This also does not satisfy the cloaking matrix
Next with three lenses, the ABCD matrix will be
By condition, setting C as zero, we get the answer which also does not suffice the required condition.
At last, getting onto four lenses, they must be arranged so that the first two must be symmetric to the other two so as to reduce the mathematical burden, which makes the ABCD matrix look like
From this and further calculation on increasing number of lenses, it can be concluded that at least four lenses must be there to make cloaking possible.
On summarising, this picture depicts the whole thing discussed intuitively.
Further developments made use of metamaterials, something that is engineered to have a property that is not found in naturally occurring materials, to build cloaking devices.
REFERENCES/CITATIONS
Choi, Joseph & Howell, John. (2014). Paraxial Ray Optics Cloaking. Optics Express. 22. 10.1364/OE.22.029465.
M. McCall, “Transformation optics and cloaking,” Contemp. Phys. 54, 273–286 (2013).
B. Zhang, “Electrodynamics of transformation-based invisibility cloaking,” Light. Sci. Appl. 1, e32 (2012).
T. Ergin, N. Stenger, P. Brenner, J. B. Pendry, and M. Wegener, “Three-dimensional invisibility cloak at optical
wavelengths,” Science 328, 337–339 (2010).
T. R. Zhai, X. B. Ren, R. K. Zhao, J. Zhou, and D. H. Liu, “An effective broadband optical ’cloak’ without
metamaterials,” Laser Phys. Lett. 10, 066002 (2013).
J. S. Li and J. B. Pendry, “Hiding under the carpet: A new strategy for cloaking,” Phys. Rev. Lett. 101, 203901
(2008).





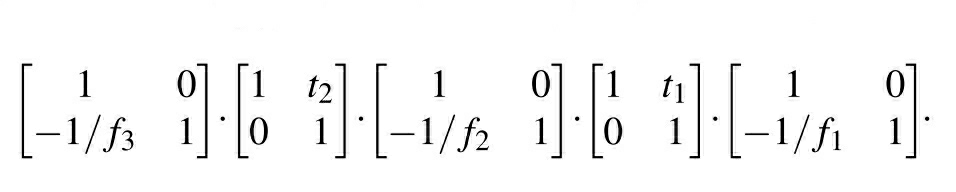











Informative!
ReplyDeleteGreat article
ReplyDelete